Modelling the airflow / Pressure map
After having drawn the shape of the wing, the airflow is modelled around the upper and lower part. Let’s suppose that the wing is currently flying in the air (or equivalently placed into a wind tunnel). The airflow is supposed to be laminar, that is to say that the airflow can be split into slices : each air molecule moves along curves that are non-intersecting, as in the following picture :
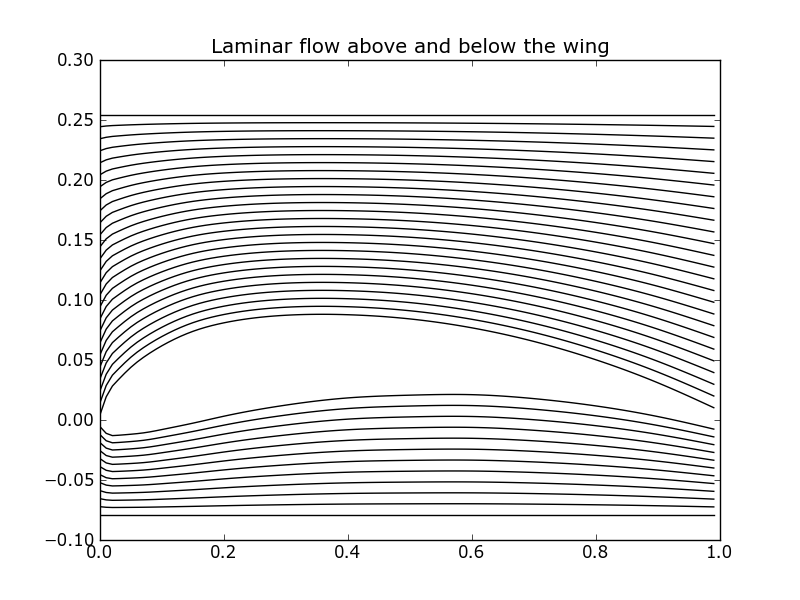
Near the airfoil, the air moves along a curve very similar to the airfoil, whereas when the air is situated further, it moves horizontally, without disturbance. The difficulty here consists in determining how the air flows between these two extreme states.
This exercise makes a number of approximations on the fluid dynamics and cannot represent the airflow in a perfectly realistic manner.
Let $h_{min}$ (resp. $h_{max}$) be the minimal (resp. maximal) height of the airfoil. In the following, we suppose that the airflow is disturbed by the wing only in a vertical interval $[3h_{min};3h_{max}]$. Out of this interval, the air flows in a rectilinear way.
Let $y=f(x)$ be the curve representing the upper surface of the wing. The family of curves describing the airflow above the wing are given by the following equations :
$$y = f_{\lambda}(x) = (1-\lambda)f(x)+\lambda \times 3h_{max} \qquad \forall \lambda \in [0;1]$$
For a fixed $\lambda$, this equation defines a curve situated between the upper side of the wing and the maximal altitude beyond which the air is not disturbed by the wing.
The pressure on each slice is computed in the following manner : the air is supposed to flow along the curves $f_\lambda$ on each part of the wing. And the air pressure as a moving fluid can be approximated with the Bernoulli law :
For the sake of simplicity, let’s suppose that $P$ is constant on the whole area. The variations of pressure are therefore linked to the variations of speed of the air. Since the air flows in a laminar manner, it takes the same time to pass through the zone (from the leading edge to the trailing edge of the wing), independently of the slice along which it flows. As a consequence, it is possible to compute the speed of the air as a simple function of the length of the slice.
The force induced by the air on the wing is merely due to the static pressure : it is normally weaker on the upper part of the wing than on the lower part. This difference induces a force, named the lift, that sustains the plane in the air during its flight. If we are only interested by dynamic pressure, it is possible to compute a map of this pressure around the wing that looks like the following :
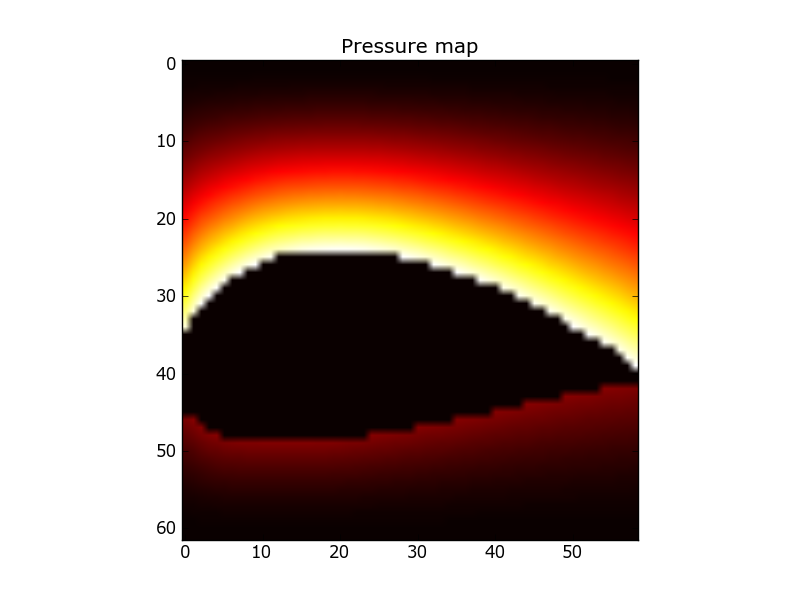
Black areas correspond to zones where the air is not disturbed, and lighter areas correspond to zones where the air must travel along a longer path. It can be noticed that the air flows faster above than below.
- Question :
- Write a function performing the computation of a pressure map around the wing.
Attention will be paid to the algorithmic complexity of the function in order to get a reasonable resolution in short amount of time.