Système proie-prédateur de Lotka-Volterra
Dans cette partie, on s’intéresse à la modélisation de l’évolution de la population d’une ou plusieurs espèces dans un milieu naturel. Les équations différentielles décrites ici sont des modèles de population. Considérons la fonction $N(t)$ décrivant la variation de la population d’un ensemble d’individus au cours du temps. Les premiers modèles de population (dits malthusiens, car dûs à Malthus à la fin du XVIIIème siècle) décrivaient ainsi les variations de cette fonction :
$$ \begin{align*} \frac{dN(t)}{dt} & = \textrm{naissances} - \textrm{morts} \\\ & = bN(t)-dN(t) \\\ & = \gamma N(t) \end{align*}, \quad b,d > 0$$
Néanmoins, cette approche n’est pas vraiment réaliste (même si la croissance de la population humaine ne contredit pas effectivement le modèle), et Verhulst a proposé un autre modèle de population auto-limitant :
$$\frac{dN(t)}{dt} = \displaystyle\gamma N(t) \left( 1 - \frac{N(t)}{\kappa} \right), \quad \gamma, \kappa > 0$$
- Questions :
- Expliquer en quoi ces deux équations différentielles peuvent modéliser les variations d’une population, et en particulier à quoi correspondent les constantes apparaissant à l’intérieur.
- Résoudre ces équations différentielles en utilisant la méthode de votre choix, et en choisissant différents points de départ crédibles.
Ces modèles peuvent être modifiés à loisir, mais lorsque l’on veut décrire un écosystème de manière un peu plus riche, il est possible de modéliser les interactions de deux populations proies/prédateurs : $N(t)$ est une population de proies et $P(t)$ est une population de prédateurs. Le modèle de Lotka-Volterra est le suivant :
$$ \begin{cases} \frac{dN(t)}{dt} = N(t) (a-bP(t)) \\\ \frac{dP(t)}{dt} = P(t) (cN(t)-d) \end{cases}, \quad a;b;c;d > 0$$
- Questions :
- Expliquer en quoi ces deux équations peuvent-elles modéliser un écosystème proie/prédateur.
- Résoudre numériquement ce système d’équations différentielles en utilisant une méthode de votre choix, et en choisissant différents points de départ crédibles. Tracer les variations des deux populations au cours du temps.
- Tracer sur une courbe les variations du couple $(N(t),P(t))$ au cours du temps. Quels types de solutions fait-on apparaître ? Quelles sont les solutions constantes ?
- Mettre en place un algorithme permettant de calculer la période de ces solutions (de manière approchée).
Lors de l’étude d’un système d’équations différentielles, on s’intéresse au comportement global des solutions, mais aussi à leur comportement local. En particulier, il est intéressant de regarder les variations entre des solutions partant de conditions initiales très proches.
- Question :
- Écrire un algorithme qui permette de tracer les solutions autour d’un point de départ donné. En fonction d’une condition initiale $y_0$, il s’agit de tracer la courbe solution en partant de $y_0$, puis les courbes solutions en partant de conditions initiales qui sont proches de $y_0$ (il est possible de les choisir dans un petit disque/rectangle centré sur $y_0$).
Le résultat pourra ressembler à :
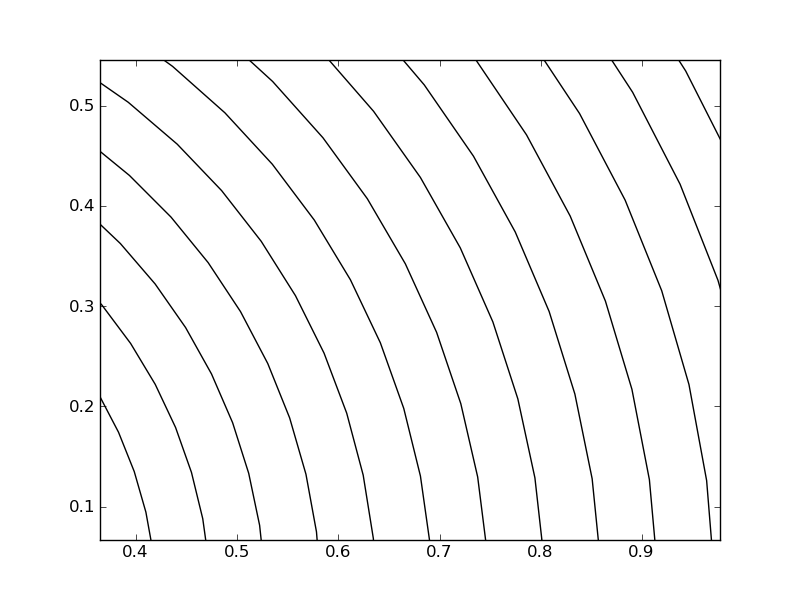
On rappelle qu’il s’agit bien d’expliquer le comportement local de l’équation différentielle, et donc que la fenêtre considérée doit être petite. De plus, il est important de ne considérer que les EDO en dimension 2, afin de montrer des courbes solutions qui ne se croisent pas.
- Questions :
- Un point singulier de l’équation différentielle est un point où toutes les dérivées s’annulent. Quels sont les points singuliers du système de Lotka-Volterra ?
- Quelle est la forme générale des diagrammes obtenus à la question 7 (en partant d’une condition initiale différente d’un point singulier) ? Quelle est la forme de ces diagrammes lorsque l’on part d’un des points singuliers de l’équation ?
(Difficile) Si l’on se replace dans le contexte d’une équation différentielle générale, à quels types de diagrammes peut-on s’attendre ?
Pour tester le comportement du système proie-prédateur, on pourra tester le programme NetLogo.