Réactions chimiques oscillantes
Usuellement, les réactions chimiques ont un comportement simple d’un point de vue thermodynamique : la réaction arrive à un équilibre stable à partir duquel on peut considérer qu’il n’y a plus d’interaction entre les réactifs. Néanmoins, il existe des réactions chimiques dites oscillantes, qui ont un comportement périodique. La plus connue de ces réactions est la réacition de Belousov-Zhabotinsky, ou encore celle de Briggs-Schauer.
Le système auquel nous nous intéressons ici est un sytème oscillant simplifié, à trois dimensions, modélisé par les équations suivantes :
$$ \begin{cases} \frac{dX(t)}{dt} = a + b Z - X - X Y^2 \\\ \frac{dY(t)}{dt} = c (X + X Y^2 - Y) \\\ \frac{dZ(t)}{dt} = d (Y - Z) \end{cases}, \quad a;b;c;d > 0 $$
Pour les conditions de la réaction, les valeurs intéressantes se situent pour $a=10$, $c=200$, $d=50$, et $b\in [0.1,0.2]$. Les valeurs initiales sont fixées à $[1; 0; 0]$. Dans cette partie, on s’intéresse au comportement de la réaction en fonction du paramètre $b$.
- Question :
- Résoudre les équations précédentes pour différentes valeurs du paramètre $b$.
Remarque : Les solutions obtenues doivent être périodiques, ou ultimement périodiques. Aucune solution ne diverge vers l’infini. Veillez à vérifier que vos calculs ne divergent pas, en prenant des pas de calculs suffisamment faibles.
Toutes les solutions ont un comportement ressemblant : premièrement, une phase de démarrage, puis une phase stable dans laquelle la fonction a un comportement périodique, ou quasi-périodique. Pour mesurer la complexité de ce comportement, nous allons définir une notion de période d’une solution : étant donné une solution $[X(t);Y(t);Z(t)]$, la période de cette solution est égale au nombre de maxima locaux de $Y(t)$ restreinte à sa phase périodique.
- Questions :
- Comment ne considérer que la phase périodique d’une solution ?
- Écrire une fonction qui, étant donné une valeur du paramètre $b$, calcule la période de la solution associée.
- Pouvez-vous exhiber des solutions de période 2 ? de période 4 ? de période 5 ? de période 3 ? Pouvez-vous exhiber des solutions de période infinie ?
- Tracer le diagramme de bifurcation de ce système dynamique, à
savoir une courbe traçant les pics de la solution en fonction du
paramètre $b$.
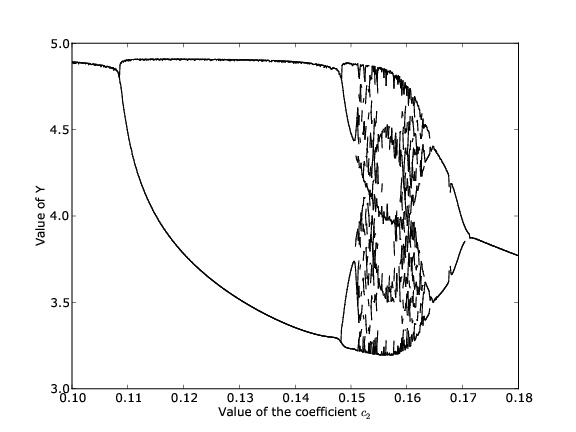
- Dans leur article Period 3 implies Chaos, Li et Yorke montrent qu’un système dynamique exhibant des solutions de période 3 devait nécessairement contenir des solutions chaotiques. Est-ce le cas du présent système ? Et sinon, est-ce tout de même un système chaotique ?
- En quoi la modélisation numérique d’un système dynamique chaotique est elle difficile ?